Ensemble Modelling
Uncertainty is an inherent part of modelling. Models by definition are simplified representations of reality - as such they are all wrong. Being wrong doesn't necessarily make them useless, but it helps to have some idea about how wrong they are for them to be most useful. That's why we should always try to provide some means to assess the uncertainty in our models output. Producing multiple realisations of a model and its results - a model ensemble - is one way to do this.
Depending on our model we can use ensemble methods to examine four different sources of modelling uncertainty:
a) Model Structure: how appropriate are our model variables, relationships and rules?
b) Model Parameters: what numerical values appropriately represent the strengths of relationships between variables?
c) Initial Conditions: how does our uncertainty in the initial state of the system we are modelling propagate through the model to the output?
d) Boundary Conditions: how do alternative (uncertain) scenarios of events that perturb our model influence output?
In their recent paper, Arujo and New show how ensemble modelling might be used to assess the impacts of these different kinds of uncertainty on model output. They advocate the use of multiple models within an ensemble forecasting framework and argue that more robust forecasts can be achieved via the appropriate analysis of ensemble forecasts. This is important because projections between different models can be so variable as to compromise their usefulness for guiding policy decisions. For example, upon examining nine bioclimatic models for four South African plant species, Pearson et al. found that for different scenarios of future climate predicted changes in species distribution varied from 92% loss to 322% gain between the different models! It's uncertainty like this that stifles debate about the presence and impacts of anthropogenic climate change. Araujo and New go on to discuss the uses and limitations of ensemble modelling for supporting policy decisions in biodiversity conservation.
In a previous post I discussed how Bayesian methods can be used to examine uncertainty in model structure. I've been using Bayesian Model Averaging to help me identify which are the most appropriate predictors of local winter white-tailed deer density for our UP Forest project. Using the relationships developed via that modelling process I've produced spatial estimates of deer density in northern hardwood stands for a section of our study area (example below).
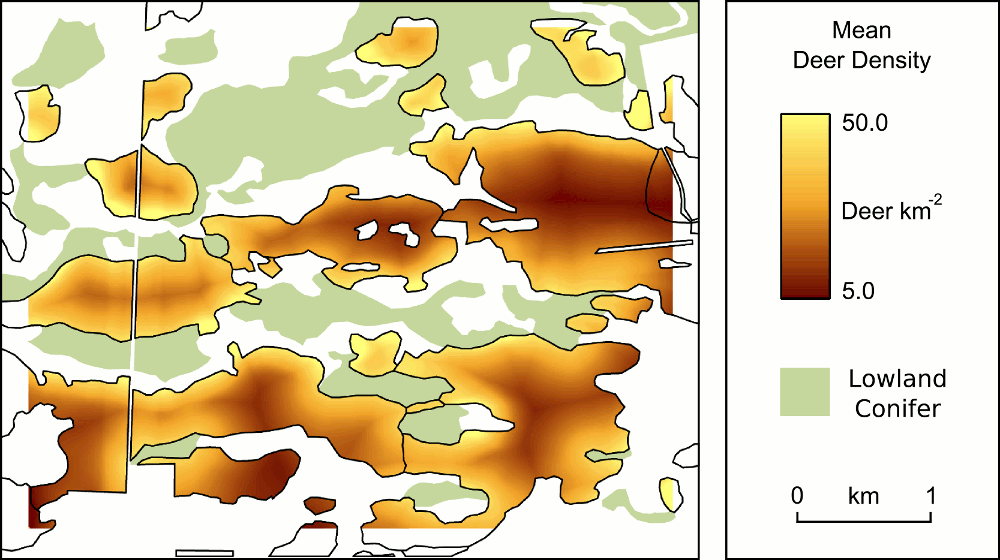
Hopefully forest managers will find this sort of modelling useful for their planning (I'll ask them sometime). However, I think this sort of product will be even more useful if I can provide the managers with a spatial estimate of uncertainty in the deer density estimates. This is important not only to emphasise that there is uncertainty in the model results generally, but also to highlight where (in the landscape) the model is more or less likely to be correct. Here's the uncertainty map corresponding with the deer density estimate map above.
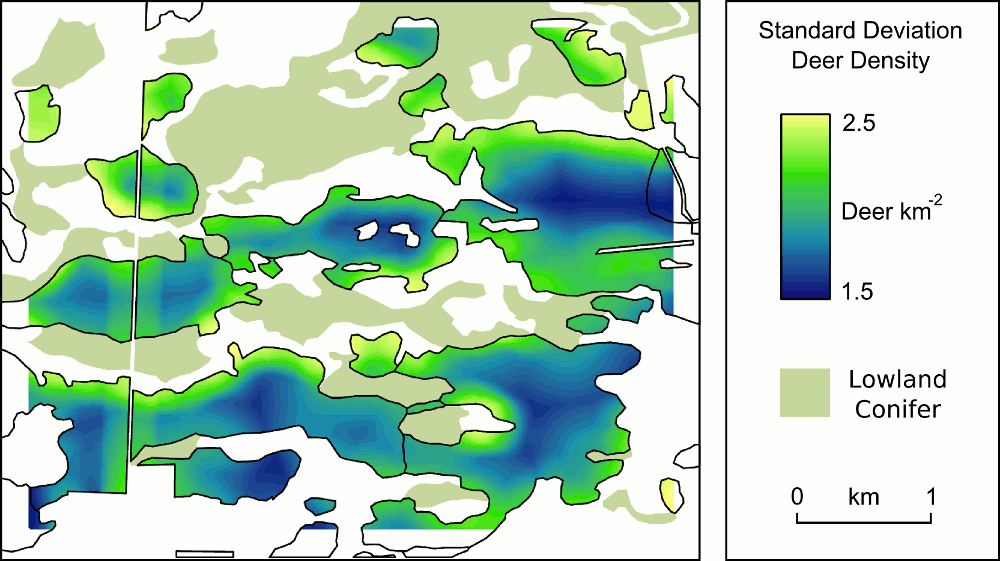
In this map the lighter colours (yellows and greens) indicate less certainty in the deer density estimate at that point. If managers were to take action in this landscape to reduce deer densities they could use a combination of the maps to find locations where deer densities are estimated to be high with low uncertainty.
To be more specific, the uncertainty map above is the standard deviation of 1,000 deer density estimate maps (correspondingly the deer density map is the mean of these 1,000 models). For each of the 1,000 deer density estimates I used slightly different model parameter values, each chosen with a certain probability. These 1,000 realisations are my model ensemble. The probability a value would be chosen for use as a parameter in any of the 1,000 models was specified by a (normal) probability distribution which came from the mean and standard deviation provided by the original Bayesian regression model. To produce the 1,000 models and sample their parameter values from a probability distribution I wrote my own program which made use of the standalone R math libraries built by Chris Jennings.
Appropriately representing and communicating uncertainty in model output is vital if models and modelling is to be useful for non-modellers (e.g., policy-makers, natural resource managers, etc.). Spatial ensemble modelling helps us to do this by identifying locations where we are more or less confident about our model output.
Depending on our model we can use ensemble methods to examine four different sources of modelling uncertainty:
a) Model Structure: how appropriate are our model variables, relationships and rules?
b) Model Parameters: what numerical values appropriately represent the strengths of relationships between variables?
c) Initial Conditions: how does our uncertainty in the initial state of the system we are modelling propagate through the model to the output?
d) Boundary Conditions: how do alternative (uncertain) scenarios of events that perturb our model influence output?
In their recent paper, Arujo and New show how ensemble modelling might be used to assess the impacts of these different kinds of uncertainty on model output. They advocate the use of multiple models within an ensemble forecasting framework and argue that more robust forecasts can be achieved via the appropriate analysis of ensemble forecasts. This is important because projections between different models can be so variable as to compromise their usefulness for guiding policy decisions. For example, upon examining nine bioclimatic models for four South African plant species, Pearson et al. found that for different scenarios of future climate predicted changes in species distribution varied from 92% loss to 322% gain between the different models! It's uncertainty like this that stifles debate about the presence and impacts of anthropogenic climate change. Araujo and New go on to discuss the uses and limitations of ensemble modelling for supporting policy decisions in biodiversity conservation.
In a previous post I discussed how Bayesian methods can be used to examine uncertainty in model structure. I've been using Bayesian Model Averaging to help me identify which are the most appropriate predictors of local winter white-tailed deer density for our UP Forest project. Using the relationships developed via that modelling process I've produced spatial estimates of deer density in northern hardwood stands for a section of our study area (example below).

Hopefully forest managers will find this sort of modelling useful for their planning (I'll ask them sometime). However, I think this sort of product will be even more useful if I can provide the managers with a spatial estimate of uncertainty in the deer density estimates. This is important not only to emphasise that there is uncertainty in the model results generally, but also to highlight where (in the landscape) the model is more or less likely to be correct. Here's the uncertainty map corresponding with the deer density estimate map above.

In this map the lighter colours (yellows and greens) indicate less certainty in the deer density estimate at that point. If managers were to take action in this landscape to reduce deer densities they could use a combination of the maps to find locations where deer densities are estimated to be high with low uncertainty.
To be more specific, the uncertainty map above is the standard deviation of 1,000 deer density estimate maps (correspondingly the deer density map is the mean of these 1,000 models). For each of the 1,000 deer density estimates I used slightly different model parameter values, each chosen with a certain probability. These 1,000 realisations are my model ensemble. The probability a value would be chosen for use as a parameter in any of the 1,000 models was specified by a (normal) probability distribution which came from the mean and standard deviation provided by the original Bayesian regression model. To produce the 1,000 models and sample their parameter values from a probability distribution I wrote my own program which made use of the standalone R math libraries built by Chris Jennings.
Appropriately representing and communicating uncertainty in model output is vital if models and modelling is to be useful for non-modellers (e.g., policy-makers, natural resource managers, etc.). Spatial ensemble modelling helps us to do this by identifying locations where we are more or less confident about our model output.
Labels: MichiganUP, Modelling, Statistical

This work by James D.A. Millington is licensed under a Creative Commons Attribution-Noncommercial-Share Alike 3.0 United States License.


0 Comments:
Post a Comment
<< Home